[컴개실] Ch.2 - Bits, Data Types, and Operations

Bits and Data Types

컴퓨터의 비트(bit)는 전기 신호를 이용해 정보를 저장한다. '신호가 있음'과 '없음'은 각각 하나의 상태를 나타낸다고 할 수 있고, 이런 상태를 저장할 수 있는 비트가 N개 있다면, 모든 경우의 수인 $2^N$가지 상태를 표현할 수 있다. (8 bit=1 byte, 4 bit=1 nibble이라 한다.)

여기에, 각 경우의 수를 어떻게 해석해야 하는지에 대한 맥락(인코딩)이 주어진다면, 컴퓨터는 비트의 조합으로 정수, 실수, 문자, 소스 코드, 멀티미디어 데이터 등 다양한 의미의 정보를 표현할 수 있다.

이런 맥락을 제공하는 것이 자료형(data type)이다. 이의 예시로는 정수 자료형, 부동 소수점, ASCII 코드 등이 있다.

Bit-Level Operations

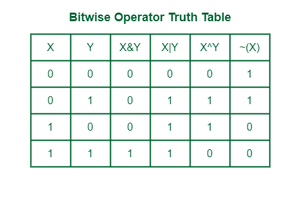
비트를 이용해 할 수 있는 기본적인 연산들에는 하나의 비트 혹은 비트열을 반전시키는 NOT 연산(~)이 있고, 두 비트 혹은 두 비트열의 이항 연산인 AND(&), OR(|), XOR(^)이 있다. 이 연산들의 진리표는 아래와 같다.

Shift(<<, >>) 연산은 비트열에서 각 비트의 위치를 옆으로 옮기는 연산을 말한다.

예를 들어 x = 010110에서 x<<2 연산을 하면 011000이 된다.

Integer Representations

컴퓨터는 하나의 비트를 하나의 2진수 자릿수로 취급하여, 2진수로 정수를 저장한다. 0번부터 w-1번까지 총 w개의 비트에 저장된 데이터를 양의 정수로 인코딩하는 방법은 다음과 같다. $x_k$ 는 k번째 비트에 해당하는 값(0 또는 1)을 의미한다.

$\displaystyle x=\sum_{k=0}^{w-1}x_k 2^k$

예를 들어 0100은 5, 1101은 13로 인코딩된다.

그런데, 음의 정수도 표현하기 위해선 어떻게 해야 할까? 즉, 양의 정수와 음의 정수, 0을 모두 표현할 수 있으면서 정수들끼리 연산하기 편리하려면 정수를 어떻게 인코딩해야 할까?

Two's complement(2의 보수법)이 좋은 방법이다. 이 방식은 Most Significant Bit, 즉 가장 자릿수가 큰 비트의 부호를 반대로 하여 더해 주는 방법인데, 인코딩 방식이 간단하고 부호가 없는 정수의 덧셈, 곱셈 방식을 음수에도 일관적으로 적용할 수 있다!

0번부터 w-1번까지 총 w개의 비트에 저장된 정수를 Two's complement로 표현하면 다음과 같다.

$\displaystyle x=-x_{w-1}w^{w-1}+\sum_{k=0}^{w-2}x_k 2^k$

위의 수식에서 Most Significant Bit에 해당하는 항에 마이너스를 붙인 것 뿐이다. 예를 들어, 음수를 포함한 정수를 4-bit로 인코딩하는 경우 0110은 6, 1101은 -3을 의미한다.

Operations on Bits

비트열로 표현된 정수의 덧셈과 뺄셈은, 단순히 2진수를 더하는 연산이다. 특히 뺄셈은 빼는 수를 음수로 바꾸어 더하면 된다.

비트열의 비트 수를 늘려 더 큰 숫자의 범위를 표현하고 싶을 때 Sign Extension을 할 수 있다. 2의 보수법으로 표현된 정수의 경우, Sign Extension을 하기 위해선 늘리고 싶은 만큼, 원래 비트열의 Most Significant Bit를 왼쪽에 붙여넣으면 원래의 값을 유지할 수 있다. 예를 들어 0110 -> 00000110, 1010 -> 11111010 과 같이 늘린다.

비트에는 논리 연산을 할 수도 있다. 논리 연산이란 '참', '거짓'의 두 가지 값만을 가질 수 있는 상태들을 연산하는 것이다. 논리적 상태의 값을 뒤집는 NOT(!), 두 상태가 모두 참일 때만 '참'을 내놓는 AND(&&), 하나라도 참이면 '참'을 내놓는 OR(||), 그리고 하나만 참일 때 '참'을 내놓는 XOR이 있다. 정수로 인코딩된 비트열을 대상으로 연산하는 경우, 컴퓨터는 0을 '거짓'으로, 0이 아닌 모든 값을 '참'으로 인식한다.

Integer Operations

컴퓨터는 어떻게 비트열로 표현된 정수에 대한 산술 연산을 할까?

Negation: 일단 마이너스(-) 부호를 붙여 보자. 우선 2의 보수로 표현된 정수에서 ~x + x == -1라는 것을 관찰할 수 있다. 이로부터 -x == ~x+1이라는 것을 보일 수 있다.

Unsigned Addition: 두 부호 없는 정수의 덧셈은 단순한 2진수의 덧셈이다. 단, 올림이 발생해 정해진 비트열의 길이를 초과할 경우 그 올림은 버려진다. 다른 말로, 정수의 덧셈은 덧셈을 한 후 모듈러 연산이 되는 것이라 할 수 있다. ($UAdd_w(u,v) = (u+v)mod2^w$) 이것으로 인해 덧셈 결과가 true sum과 달라지는 것을 overflow라 한다.

Two's Complement addition: 부호가 있는 정수도 unsigned addition과 완전히 같은 방식으로 작동한다. 이것이 2의 보수법을 사용하는 이유이다!

Unsigned Multiplication: 덧셈과 마찬가지로, 곱셈 연산의 결과가 비트열의 정해진 길이를 초과하면 앞부분의 비트는 버린다. ($UMult_w(u,v)=(u*v)mod2^w$)

Shift: 부호 없는 정수형에서, shift left와 shift right는 이진수의 자릿수를 옮기는 연산이므로 각각 2의 제곱을 빠르게 곱하고 나누는 연산을 한다. 2의 보수로 표현된 음수에서는 shift right를 그냥 하게 되면 갑자기 양수가 되어 버리므로 (ex: 1110 -> 0111) Most Significant Bit를 가장 왼쪽 비트에 채워넣어 부호를 유지한다. (ex: 1110 -> 1111)

Floating Point(부동 소수점)

정수가 아닌 실수는 어떻게 표현할까? 2진수로 소수점 아래 자릿수들을 저장하는 건(Binary Fractional Numbers) 좋은 생각은 아니다. 정수 표현처럼 표현 가능한 범위와 precision이 크게 제한되어 있을 것이기 때문이다.

큰 수부터 절댓값이 1 이하인 작은 수까지 넓은 범위의 실수를 표현하기 위해, 소수점의 위치를 마음대로 조절할 수 있으면 좋을 것이다. 즉 소수점(point)이 자유자재로 부동(float)할 수 있으면 좋을 것이다. 이것을 가능케 하는 것이 floating point 형이고, 현재 컴퓨터가 실수를 표현하는 데는 IEEE 754 표준이 사용되고 있다.

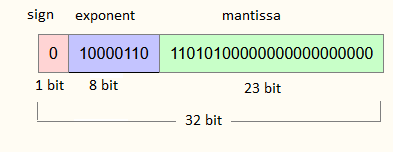
IEEE 754 표준은, 실수를 지수부(exponent)와 소수부(mantissa)로 나누어 저장한다. 십진수로 예를 들면 123.4를 1.234 * 10²로 표현하여, '1234'와 '2'를 저장하는 식이다.

이러한 저장 방식으로 인해, 지수부가 커질수록 floating point가 저장할 수 있는 한 수에서 가장 가까운 다음 수와의 차이가 커진다는 특징이 있다.

References

1. Yale N. Patt, Sanjay J. Patel. 『Introduction to Computing Systems: From Bits&Gates to C/C++ and Beyond』. 3rd ed. McGraw Hill(2019). p19-50